Size of the Sun

Sunrise June 8 2004

Video Link -  
Includes directions for setting up and using this equipment.

If we know the distance to the sun we can  construct some simple equipment that will allow us to calculate the size of the sun.
The average distance to the sun  is ~ 149, 595, 390 km. (~ 150, 000, 000 km)

Constructing the equipment:



make a pinhole

Shove a push pin through a small  (2 cm x 2 cm)  piece of aluminum foil.
Aluminum cookie sheets work well.

pinhole

Fold a small card (~ 8 cm X 15 cm) as shown.
Punch a hole through the upper part of the card and  tape the aluminum piece with pinhole over the hole in the card.

graph paper on card

Fold a small piece of card (~ 6 cm x 15 cm) as shown.
Glue a small piece of graph paper to the card.

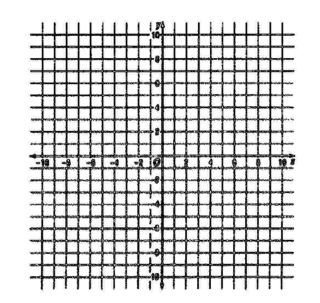
sample grid
If you don't have any graph paper, print this image.
("Right Click" then choose save image)
You can glue it to the above card.

After you print the graph paper measure the distance between the lines.
Ideally the distance is 1 or 2 mm, if not use a graphics program to make the image larger or smaller.
Experiment until you get the size right.

graph meter stick

Tape the graph card to one end of  a meter stick as shown.

pinhole on meter stick

Tape the pinhole card to the other end of the meter stick.

sunshine on pinhole

Align the meter stick so that the sun shines through the pinhole onto the graph paper.
Carefully count the number of  lines that the image spans on your graph paper.
If you know how far apart the lines are on the graph paper you can calculate the size of the image.

pinhole image

This is what the sun's image looks like on the graph paper.
The lines on this graph paper are 2mm apart.
The sun's image is ~ 9.5 mm.

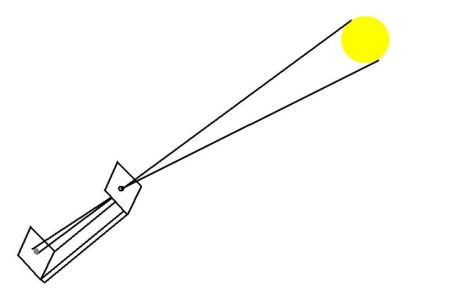
sun shines through pinhole
Your equipment has created two similar isosceles triangles.
(Completing this project requires some knowledge of basic geomtry and algebra)

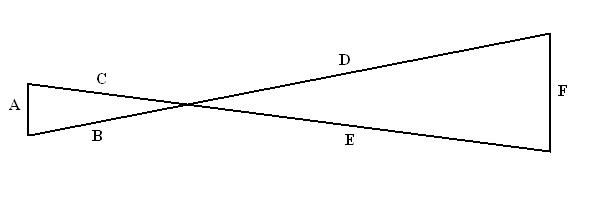
similar triangles
Isosceles triangle ABC is similar to triangle FED.
This means the angles are the same.
Angle B-C = Angle E-D
Angle A-B = Angle E-F = Angle A-C = Angle D-F


Also the ratios:   A/B  =  F/D

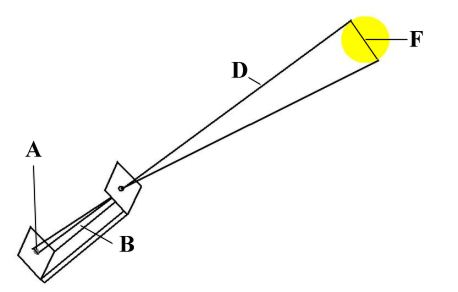label

You know 3 of the values in the above drawing.

A = the diameter of the sun's image (~ 9.5 mm)
B = the meter stick (1 meter or 1000 mm)
D = the distance to the sun (150, 000, 000 km)
F = diameter of sun (unknown)


Remember A/B = F/D
or
F = (A x D)/B

F = (9.5 mm x 150000000 km)/1000 mm

F = 1 425 000 km
Estimated diameter of sun = 1 425 000 km

Actual diameter of sun = 1 391 978 km
Extra Information:

We know the earth's orbit around the sun is elliptical.   During winter in the Northern Hemisphere we are close to the sun, at this time of year the  minimum distance to the sun is 147, 085, 800 km. It is the tilt of the earth's axis that creates the colder temperature of winter, not distance to the sun.

During summer in the Northern Hemisphere we are far from the sun, the maximum distance to the sun is  152, 104, 980 km.

Average distance to sun: 149,595,390 km  

If you are doing this project in the summer or winter you may want to adjust the value you use for distance to the sun.

You can increase the accuracy of this method by increasing the distance from the pinhole to the sun's image. The resulting larger image is easier to measure.


Return